重新看了一段时间的数据结构和算法，写点总结和梳理。

使用 Python 和 C/C++/Java 进行描述。

第3章排序算法

3.1 简单排序算法

3.1.1 冒泡排序

两重循环的交换排序，无需细述。

将列表分为顶部的有序区（初始为空）和底部的无序区（初使为整个列表）；

每轮排序在无序区中，从底端到顶端两两比较，将该区域的最小元素一步步交换（冒泡）到顶端，最后并入有序区作为新底端。

剩下的无序区循环进行比较直至整体有序。

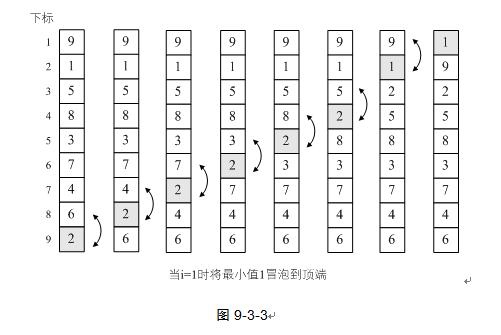
平均/最差时间复杂度：O(n^2)

最好时间复杂度：O(n)

空间复杂度：O(1)

稳定性：稳定

（稳定指：原序列中若有元素 a、b 值相同，且 a 在 b 之前；则排序后 a 仍在 b 之前）

# Python 实现
def bubble_sort(array):
    # i为轮次，也是有序区的长度，当有序区长度为N-1时不再比较。
    for i in range(len(array)-1):
        # 从最后的数字开始两两比较，到 i+1 与 i 对比并交换完成后为止。
        for j in range(len(array)-1,i,-1):
            if array[j-1]>array[j]:
                array[j-1], array[j] = array[j], array[j-1]

// C 实现
void Swap(ElemType *x, ElemType *y){
  ElemType temp = *x;
  *x = *y;
  *y = temp;
}

void BubbleSort(ElemType *A, int count){
  for(int i = 0; i<count-1; i++){
    for(int j = count-1; j>i; j--){
      if(A[j-1]>A[j]) Swap(&A[j], &A[j-1]);
    }
  }
}

// C++ 实现
template <typename ElemType>
void BubbleSort(vector<ElemType> &A){
  for(int i = 0; i<A.size()-1; i++){
    for(int j = A.size()-1; j>i; j--){
      if(A[j-1]>A[j]) swap(A[j], A[j-1]);
    }
  }
}

// Java
public static <T extends Comparable<T>> void bubbleSort(T[] arr){
    for(int i = 0; i<arr.length; i++){
        for(int j = arr.length-1; j>i; j--){
            if(arr[j].compareTo(arr[j-1])>0){
                T temp = arr[j];
                arr[j] = arr[j-1];
                arr[j-1] = temp;
            }
        }
    }
}

3.1.2 插入排序

从第二个元素开始，依次扫描序列，对于扫描到的每一个元素，均与该元素之前的序列对比，并按照大小顺序插入到该序列中的正确位置

平均/最差时间复杂度：O(n^2)

最好时间复杂度：O(n)

空间复杂度：O(1)

稳定性：稳定

# Python 实现
def insertion_sort(array):
    # 第一个元素已经完成插入，从第二个元素开始
    for i in range(1,len(array)):
        # 将「无序区」的第一个元素取出作为 key，准备插入
        key = array[i]
        # 从「有序区」的最后一个元素开始比较
        j = i-1
        while j>=0 and array[j]>key:
            # 每个大于 key 的元素都后移一个位置
            array[j+1] = array[j]
            j -= 1
        # 腾出来的位置就是插入 key 的位置
        array[j+1] = key

// C 实现
void InsertionSort(ElemType *A, int count){
  ElemType key;
  // 第一个元素已经完成插入，从第二个元素开始
  for(int i=1; i<count; i++){
    // 将「无序区」的第一个元素取出作为 key，准备插入
    key = A[i];
    // 从「有序区」的最后一个元素开始比较
    int j;
    for(j=i-1; j>=0 && A[j]>key; j--){
      // 每个大于 key 的元素都后移一个位置
      A[j+1] = A[j];
    }
    // 腾出来的位置就是插入 key 的位置
    A[j+1]=key;
  }
}

// C++ 实现
template <typename ElemType>
void InsertionSort(vector<ElemType> &A){
  ElemType key;
  // 第一个元素已经完成插入，从第二个元素开始
  for(int i=1; i<A.size(); i++){
    // 将「无序区」的第一个元素取出作为 key，准备插入
    key = A[i];
    // 从「有序区」的最后一个元素开始比较
    int j;
    for(j=i-1; j>=0 && A[j]>key; j--){
      // 每个大于 key 的元素都后移一个位置
      A[j+1] = A[j];
    }
    // 腾出来的位置就是插入 key 的位置
    A[j+1]=key;
  }
}

// Java
// 基本同 C++
public static <T extends Comparable<T>> void insertionSort(T[] arr){
    T key;
    for(int i=1; i<arr.length; i++){
        key = arr[i];
        int j;
        for(j=i-1; j>=0 && A[j].compareTo(key)<0; j--){
            arr[j+1] = arr[j];
        }
        arr[j+1] = key;
    }
}

3.1.3 选择排序

将列表分为左侧的有序区（初始为空）和右侧的无序区（初使为整个列表）；

每轮排序在无序区中，寻找到最小元素，并直接与有序区末尾的下一个元素交换。反复进行直到排序完成。

平均/最差/最好时间复杂度：O(n^2)

空间复杂度：O(1)

稳定性：不稳定

# Python 实现
def selection_sort(array):
    # 「无序区」初始为整个列表
    # 倒数第二个元素排列完成后，最后一个元素一定是最大的元素
    for i in range(0,len(array)-1):
        # 寻找「无序区」最小元素
        # （第 i 次循环时，「无序区」的最小元素就是全序列中第 i 大的元素）
        index_min = i
        for j in range(i+1,len(array)):
            if array[j]<array[index_min]:
                index_min = j
        # 与「有序区」的下一个元素交换
        array[i], array[index_min] = array[index_min], array[i]

// C 实现
void Swap(ElemType *x, ElemType *y){
  ElemType temp = *x;
  *x = *y;
  *y = temp;
}

void SelectionSort(ElemType *A, int count){
  int index_min;
  // 「无序区」初始为整个列表
  for(int i=0; i<count-1; i++){
    // 寻找「无序区」最小元素
    // （第 i 次循环时，「无序区」的最小元素就是全序列中第 i 大的元素）
    index_min = i;
    for(int j=i+1; j<count; j++){
      if(A[j]<A[index_min]) index_min = j;
    }
    // 与「有序区」的下一个元素交换
    Swap(&A[index_min], &A[i]);
  }
}

// C++ 实现
template <typename ElemType>
void SelectionSort(vector<ElemType> &A){
  int index_min;
  // 「无序区」初始为整个列表
  for(int i=0; i<A.size()-1; i++){
    // 寻找「无序区」最小元素
    // （第 i 次循环时，「无序区」的最小元素就是全序列中第 i 大的元素）
    index_min = i;
    for(int j=i+1; j<A.size(); j++){
      if(A[j]<A[index_min]) index_min = j;
    }
    // 与「有序区」的下一个元素交换
    swap(A[index_min], A[i]);
  }
}

// Java
// 基本同 C++
public static <T extends Comparable<T>> void selectionSort(T[] arr){
    int indexMin;
    for(int i=0; i<arr.length-1; i++){
        indexMin = i;
        for(int j=i+1; j<arr.length; j++){
            if(arr[j].compareTo(arr[indexMin])<0) indexMin = j;
        }
        T temp = arr[indexMin];
        arr[indexMin] = arr[i];
        arr[i] = temp;
    }
}

3.2 希尔排序

希尔排序，也称递减增量排序算法，是对插入排序的改进，主要基于插入排序的两个性质：

对于基本有序的序列进行插入排序时，效率很高，接近线性
插入排序通常是低效的，因为每次只能将数据移动一位

希尔排序首先取一个增量 Step，然后将序列分组，所有间距为 Step 的元素划入同一组，然后对每一组进行插入排序。

然后不断减少增量 Step 来进行多轮排序；最终增量减小到 1 时，即为普通的插入排序。（此时数据已经基本有序，插入排序的速度将非常快）

3.3 堆排序

将所有的元素建立成一个最小/最大堆，然后依次弹出堆首元素并组成一个新表，排序完成。

建立一个最大堆，每次弹出元素变为「交换堆首和堆尾，然后减小堆的尺寸」，可以实现原地排序。

适合 n 大的情况

3.3.1 时间复杂度：O(nlogn)

平均/最好/最差：O(nlogn)

3.3.2 空间复杂度：O(1)

原地：O(1)

3.3.3 稳定性：不稳定

3.3.4 实现

# Python 实现
# 非原地简易实现，可直接使用 heapq 模块
from heapq import heapify, heappop
def heap_sort(array):
    heapify(array)
    array[:] = [heappop(array) for _ in range(len(array))]

# 原地实现
def heap_sort(array):
    '''原地堆排序'''
    def shift_down(root):
        '''维护最大堆'''
        while True:
            child = 2 * root + 1
            if child>last:
                break
            # 寻找最大子节点
            if child<last and array[child+1]>array[child]:
                child += 1
            if array[root]<array[child]:
                array[root],array[child] = array[child], array[root]
                root = child
            else:
                break
                
    last = len(array)-1
    root = (last-1)//2
    # 建立最大堆
    while root:
        root -= 1
        shift_down(root)
    # 堆首交换到堆尾，并减少堆的长度
    while last:
        array[0], array[last] = array[last], array[0]
        last -= 1
        shift_down(0)

// C 实现
void Swap(ElemType *x, ElemType *y){
  ElemType temp = *x;
  *x = *y;
  *y = temp;
}
void ShiftDown(ElemType *A, int root, int last){
  /*维护最大堆*/
  for(;;){
    int child = 2 * root + 1;
    if(child>last) break;
    // 寻找最大子节点
    if(child<last && A[child+1]>A[child]) child++;
    if(A[root]<A[child]){
      Swap(&A[root], &A[child]);
      root = child;
    }
    else break;
  }
}
void HeapSort(ElemType *A, int n){
  /*原地堆排序*/
  int last = n - 1;
  int root = (last-1)/2;
  // 建立最大堆
  while(root>=0){
    ShiftDown(A, root--, last)
  }
  // 堆首交换到堆尾，并减少堆的长度
  while(last>0){
    Swap(&A[0], &A[last]);
    ShiftDown(A, 0, --last);
  }
}

// C++实现
// 直接使用 STL
template <typename T>
void HeapSort(vector<T>& A){
    make_heap(A.begin(), A.end());
    sort_heap(A.begin(), A.end());
}
// 或者直接实现参考 C 实现

// Java 实现
// 参考 C 实现
private static <T extends Comparable<T>> void shiftDown(T[] arr,int root,int last){
    for(;;){
        int child = 2 * root +1;
        if(child>last) break;
        if(child<last && arr[child+1].compareTo(arr[child])>0) child++;
        if (arr[root].compareTo(arr[child])<0){
            T temp = arr[root];
            arr[root] = arr[child];
            arr[child] = temp;
        }
        else break;
    }
}

public static <T extends Comparable<T>> void heapSort(T[] arr){
    int last = arr.length-1;
    int root = (last-1)/2;
    while(root>=0){
        shiftDown(arr, root--, last);
    }
    while(last>0){
        T temp = arr[0];
        arr[0] = arr[last];
        arr[last] = temp;
        shiftDown(arr, 0, --last);
    }
}

3.4 快速排序

通过分治法，取基准值，将序列分区为小于/大于基准值的两个子序列。然后对子序列递归排序。

快速排序适合序列长度（n）较大的情况。

3.4.1 基准值的选择

1）不合适的取法

不建议直接选择首/尾元素作为基准值。

否则，在反序/顺序的情况下，会产生劣质分割。

2）随机数法

通常可以使用随机数选择基准值，但产生随机数的消耗较大。多数情况下，随机数法即可很好的满足需求。

3）三数取中法

更细致的方式是，取三个元素（通常取下标值左、中、右对应的元素），将三个元素进行原地排序，把其中的中位数作为基准值。

例如，序列 [8, 1, 4, 9, 6, 3, 5, 2, 7, 0]，left、center、right 的值为 8、6、0。

排序后，序列变为 [0, 1, 4, 9, 6, 3, 5, 2, 7, 8]，并取中位数 6 为 pivot。

因为取中位数的过程中已经对这三个数进行了原地排序，所以后续排序时无需再调整 left 和 right 的对应值。

3.4.2 非原地排序

当对空间不敏感时，可以使用非原地排序，代码会非常简洁（虽然无实用价值）。

# Python 实现
# 随机数法，非原地快排
from random import choice
def quick_sort(array):
    if len(array)<=1:
        return array
    small, pivots, large = [], [], []
    pivot = choice(array)
    # 分别找出比 pivot 小的，比 pivot 大的，以及等于 pivot 的元素列表
    for item in array:
        if item < pivot:
            small.append(item)
        elif item > pivot:
            large.append(item)
        else:
            pivots.append(item)
    # 分别递归排序，然后合并
    quick_sort(small)
    quick_sort(large)
    array[:] = small + pivots + large

// C 实现
// 随机数法，非原地快排
void QuickSort(ElemType *A, int count){
    if(count<=1) return;
    ElemType pivot = A[rand() % count];
    ElemType Small[count], Large[count], Pivots[count];
  int scount = 0, lcount = 0, pcount =0;
    // 分别找出比 pivot 小的，比 pivot 大的，以及等于 pivot 的元素列表
    for(int i=0; i<count; i++){
        if(A[i]<pivot)
            Small[scount++] = A[i];
        else if(A[i]>pivot)
            Large[lcount++] = A[i];
        else
            Pivots[pcount++] = A[i];
    }
    // 分别递归排序，然后合并
    QuickSort(Small,scount);
    QuickSort(Large,lcount);
    for(int i=0;i<scount;i++) A[i]=Small[i];
    for(int i=0;i<pcount;i++,scount++) A[scount]=Pivots[i];
    for(int i=0;i<lcount;i++,scount++) A[scount]=Large[i];
}

// C++ 实现
// 没什么用，略过

// Java 实现
// 没什么用，略过

3.4.3 原地分割策略

首先将基准值 pivot 与末端元素交换，从而使得基准值离开序列，然后进行单向/双向扫描。

1）单向扫描

类似于选择排序，将序列分为左侧的「小值区」（初始为空）和右侧的「混合区」（初使为除了末端外的整个序列），序列末端为基准值；

每轮排序取「混合区」中第一个小值，将其交换至该区前端，并入「小值区」。反复进行直到「混合区」扫描完成，此时「混合区」变成「大值区」。

交换基准值与「大值区」的第一个值，则序列被分割成「小值区」、基准值、「大值区」。

详见注释。

# Python 实现
from random import randint
def quick_sort(array):
    def qs_partition(left, right):
        # 随机数法取基准值，并交换至末端，末端即基准值
        index = randint(left, right)
        array[right], array[index] = array[index], array[right]
        pivot = array[right]
        # 序列分为左侧的「小值区」[0, i] 和右侧的「混合区」(i, right)
        # 扫描「混合区」，遇到小值，则交换到该区前端，并入「小值区」, 此时 i 增长
        i = left
        for j in range(left,right):
            if array[j]<pivot:
                if i!=j: array[i], array[j] = array[j], array[i]
                i += 1
        # 扫描完成后，「混合区」即成为「大值区」，将基准值交换到「大值区」左端，基准值一定存在，且将序列正确分割
        array[i], array[right] = array[right], array[i]
        return i

    def qs_sort(left, right):
        if left<right:
            i = qs_partition(left,right)
            qs_sort(left,i-1)
            qs_sort(i+1,right)
            
    qs_sort(0,len(array)-1)

// C 实现
void Swap(ElemType *x, ElemType *y){
    ElemType temp = *x;
    *x = *y;
    *y = temp;
}

int Partition(ElemType *A, int left, int right){
    // 随机数法取基准值，并交换至末端，末端即基准值
    int i = rand() % (right - left) + left;
    Swap(&A[i], &A[right]);
    ElemType pivot = A[right];
    // 序列分为左侧的「小值区」[0, i] 和右侧的「混合区」(i, right)
    // 扫描「混合区」，遇到小于的值，则「小值区」长度加一，将其末端值与 A[j] 交换，保证仍为「小值区」
    i = left;
    for(int j = left; j<right; j++){
        if(A[j]<pivot){
            if(i!=j) Swap(&A[i], &A[j]);
            i++;
        }
    }
    // 扫描完成后，「混合区」即成为「大值区」，将基准值交换到「大值区」左端，基准值一定存在，且将序列正确分割
    Swap(&A[i], &A[right]);
    return i;
}

void QuickSortCore(ElemType *A, int left, int right){
    /*快速排序递归过程*/
    if(left<right) {
        int i = Partition(A, left, right);
        QuickSortCore(A, left, i-1);
        QuickSortCore(A, i+1, right);
    }
}
void QuickSort(ElemType *A, int count){
    QuickSortCore(A, 0, count-1);
}

// C++ 实现
template <typename ElemType>
int Partition(vector<ElemType> &A, int left, int right){
    // 随机数法取基准值，并交换至末端，末端即基准值
    int i = rand() % (right - left) + left;
    swap(A[i], A[right]);
    ElemType pivot = A[right];
    // 序列分为左侧的「小值区」[0, i] 和右侧的「混合区」(i, right)
    // 扫描「混合区」，遇到小于的值，则「小值区」长度加一，将其末端值与 A[j] 交换，保证仍为「小值区」
    i = left;
    for(int j = left; j<right; j++){
        if(A[j]<pivot){
            if(i!=j) swap(A[i], A[j]);
            i++;
        }
    }
    // 扫描完成后，「混合区」即成为「大值区」，将基准值交换到「大值区」左端，基准值一定存在，且将序列正确分割
    swap(A[i], A[right]);
    return i;
}

template <typename ElemType>
void QuickSortCore(vector<ElemType> &A, int left, int right){
    /*快速排序递归过程*/
    if(left<right) {
        int i = Partition(A, left, right);
        QuickSortCore(A, left, i-1);
        QuickSortCore(A, i+1, right);
    }
}

template <typename ElemType>
void QuickSort(vector<ElemType> &A){
    QuickSortCore(A, 0, A.size()-1);
}

// Java 实现
public static <T extends Comparable<T>> int partition(T[] arr, int left, int right){
    int i = new Random().nextInt(right-left+1) + left;
    T pivot = arr[i];
    arr[i] = arr[right];
    arr[right] = pivot;
    i = left;
    for(int j=left; j<right; j++){
        if(arr[j].compareTo(pivot)<0){
            if(i!=j){
                T temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
            i++;
        }
    }
    arr[right] = arr[i];
    arr[i] = pivot;
    return i;
}

public static <T extends Comparable<T>> void quickSortCore(T[] arr, int left, int right){
    if(left<right){
        int i = partition(arr, left, right);
        quickSortCore(arr, left, i-1);
        quickSortCore(arr, i+1 ,right);
    }
}

public static <T extends Comparable<T>> void quickSort(T[] arr){
    quickSortCore(arr, 0, arr.length-1);
}

2）双向扫描

使得 i 为0，j 为倒数第二个下标。

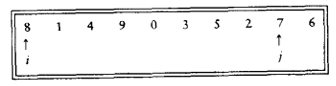
开始循环：

若 i<j，则 i 右移绕过每一个小于 pivot 的元素；若 i<j，则 j 左移绕过每一个大于 pivot 的元素；等 i、j 均停止时，。

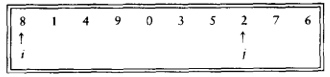
若此时仍满足 i<j，则 s[i] 为大元素，s[j] 为小元素。

交换 s[i]、s[j], 使大元素移动到右边，小元素移动到左边。

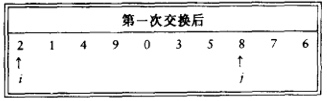
然后重复上述过程，直到不再满足 i<j 时，循环终止。

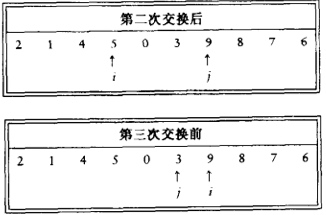
此时交换 s[i] 和 pivot：

此时序列即被 pivot 分割。

# Python 实现
# 随机数法，原地快排，双向扫描
from random import randint
def quick_sort(array):
    def qs_partition(left,right):
        '''随机数法对序列进行分区'''
        i = randint(left, right)
        array[right], array[i] = array[i], array[right]
        pivot = array[right]
        i, j = left, right
        while i!=j:
            while array[i]<=pivot and i<j:
                i += 1
            while array[j]>=pivot and i<j:
                j -= 1
            if i<j:
                array[i], array[j] = array[j], array[i]
        array[i], array[right] = array[right], array[i]
        return i
    
    def qs_sort(left, right):
        '''快速排序递归过程'''
        if left<right:
            i = qs_partition(left,right)
            qs_sort(left,i-1)
            qs_sort(i+1,right)
            
    qs_sort(0,len(array)-1)
        
# 三数中值法，原地快排，双向扫描
def quick_sort(array):
    def qs_sort2(left, right):
        '''两数排序'''
        if array[left]>array[right]:
            array[left], array[right] = array[right], array[left]
            
    def qs_sort3(left, center, right):
        '''三数排序'''
        qs_sort2(left, center)
        qs_sort2(left, right)  
        qs_sort2(center, right)
        
    def qs_median3(left, right):
        '''取三数排序返回中位数'''
        center = (left + right)//2
        qs_sort3(left, center, right)
        array[center], array[right-1] = array[right-1], array[center]
        return array[right-1]
    
    def qs_partition(left, right):
        '''对序列进行分区'''
        pivot = qs_median3(left, right)
        i, j = left, right
        while True:
            while True:
                i += 1
                if array[i]>=pivot: break
            while True:
                j -= 1
                if array[j]<=pivot: break
            if i>=j: break
            array[i], array[j] = array[j], array[i]
        array[i], array[right-1] = array[right-1], array[i]
        return i
    
    def qs_sort(left, right):
        '''快速排序递归过程'''
        if right-left>2:
            i = qs_partition(left,right)
            qs_sort(left, i-1)
            qs_sort(i+1, right)
        elif right-left==2:
            qs_sort3(left, left+1, right)
        elif right-left==1:
            qs_sort2(left, right)
            
    qs_sort(0, len(array)-1)

// C 实现
// 随机数法，原地快排，双向扫描
void Swap(ElemType *x, ElemType *y){
    ElemType temp = *x;
    *x = *y;
    *y = temp;
}

int Partition(ElemType *A, int left, int right){
    /*随机数法对序列进行分区*/
    int i = rand()%(right-left) + left;
    Swap(&A[i], &A[right]);
    ElemType pivot = A[right];
    i = left;
    int j = right;
    while(i!=j){
        while(A[i]<=pivot && i<j) i++;
        while(A[j]>=pivot && i<j) j--;
        if(i<j) Swap(&A[i], &A[j]);
    }
    Swap(&A[i], &A[right]);
    return i;
}

void QuickSortCore(ElemType *A, int left, int right){
    /*快速排序递归过程*/
    if(left<right) {
        int i = Partition(A, left, right);
        QuickSortCore(A, left, i-1);
        QuickSortCore(A, i+1, right);
    }
}

void QuickSort(ElemType *A, int count){
    QuickSortCore(A, 0, count-1);
}

// C 实现
// 三数中值法，原地快排，双向扫描
void Swap(ElemType *x, ElemType *y){
    ElemType temp = *x;
    *x = *y;
    *y = temp;
}

void Sort3(ElemType *A, int left, int center, int right){
    /*三数排序*/
    if(A[left]>A[center]) Swap(&A[left],&A[center]);
    if(A[left]>A[right]) Swap(&A[left],&A[right]);
    if(A[center]>A[right]) Swap(&A[center],&A[right]);
}

ElemType Median3(ElemType *A, int left, int right){
    /*取三数排序返回中位数*/
    int center = (left + right)/2;
    Sort3(A, left, center, right);
    Swap(&A[center], &A[right-1]);
    return A[right-1];
}

int Partition(ElemType *A, int left, int right){
    /*对序列进行分区*/
    ElemType pivot = Median3(A, left, right);
    int i = left;
    int j = right - 1;
    for( ; ; ){
        while(A[++i]<=pivot) ;
        while(A[--j]>=pivot) ;
        if(i>=j) break;
        Swap(&A[i],&A[j]);
    }
    Swap(&A[i],&A[right-1]);
    return i;
}

void QuickSortCore(ElemType *A, int left, int right){
    /*快速排序递归过程*/
    if(right-left>2) {
        int i = Partition(A, left, right);
        QuickSortCore(A, left, i-1);
        QuickSortCore(A, i+1, right);
    }
    else if(right-left==2) Sort3(A, left , left+1, right);
    else if(right-left==1 && A[left]>A[right]) Swap(&A[left],&A[right]);
}

void QuickSort(ElemType *A, int count){
    QuickSortCore(A, 0, count-1);
}

// C++ 实现
// 随机数法，原地快排，双向扫描
template <typename ElemType>
int Partition(vector<ElemType> &A, int left, int right){
    /*随机数法对序列进行分区*/
    int i = rand()%(right-left) + left;
    swap(A[i], A[right]);
    ElemType pivot = A[right];
    i = left;
    int j = right;
    while(i!=j){
        while(A[i]<=pivot && i<j) i++;
        while(A[j]>=pivot && i<j) j--;
        if(i<j) swap(A[i], A[j]);
    }
    swap(A[i], A[right]);
    return i;
}

template <typename ElemType>
void QuickSortCore(vector<ElemType> &A, int left, int right){
    /*快速排序递归过程*/
    if(left<right) {
        int i = Partition(A, left, right);
        QuickSortCore(A, left, i-1);
        QuickSortCore(A, i+1, right);
    }
}

template <typename ElemType>
void QuickSort(vector<ElemType> &A){
    QuickSortCore(A, 0, A.size()-1);
}

// Java 实现
// 随机数法，原地快排，双向扫描
public static <T extends Comparable<T>> int partition(T[] arr, int left, int right){
    int i  = new Random().nextInt(right-left+1)+left;
    T pivot = arr[i];
    arr[i] = arr[right];
    arr[right] = pivot;
    i = left;
    int j = right;
    while (i!=j){
        while (arr[i].compareTo(pivot)<=0 && i<j) i++;
        while (arr[j].compareTo(pivot)>=0 && i<j) j--;
        if (i<j) {
            T temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    arr[right] = arr[i];
    arr[i] = pivot;
    return i;
}

public static <T extends Comparable<T>> void quickSortCore(T[] arr, int left, int right){
    if (left<right){
        int i = partition(arr, left, right);
        quickSortCore(left, i-1);
        quickSortCore(i+1, right);
    }
}

public static <T extends Comparable<T>> void quickSort(T[] arr){
    quickSortCore(0, arr.length-1);
}

3.4.4 复杂度和稳定性

1）时间复杂度：O(nlogn)

平均/最好：O(nlogn) 最差：O(n^2)

2）稳定性：不稳定

3）空间复杂度

在每次递归内部的空间复杂度，取决于序列分区的方式，若通过原地交换元素分区，则为O(1)，否则最多为O(n)

然因为最好/最坏情况下，需要最多O(logn)次/O(n)递归调用；

所以原地排序需要最好O(logn)/最坏O(n)的空间

非原地排序所需空间更多，不细述。

4）特别之处

比归并排序更快的原因在于，序列分区的效率更高。

3.4.5 优化

当待排序区间较小时，采用插入排序，可以进一步提高排序效率。

3.5 归并排序

归并排序（Merge sort），是将一个序列分成两个序列，分别递归地排序，然后合并两个有序序列。

适合 n 大的情况

3.5.1 时间复杂度：O(nlogn)

平均/最好/最差：O(nlogn)

3.5.2 稳定性：稳定

3.5.3 空间复杂度：O(n)

归并排序的递归过程中，每次合并时需要一个临时空间，但因为每次递归中，合并操作都在最后一步，所以任何时刻只有一个临时空间活动，故可以共同使用同一个临时空间，该空间长度为 n，空间复杂度为 O(n)

3.5.4 实现

# Python 实现
def merge_sort(array):
    def m_merge(left_start, left_end, right_end):
        '''将两个有序子序列合并'''
        right_pos = left_end + 1
        temp_pos = left_pos = left_start
        while left_pos<=left_end and right_pos<=right_end:
            if array[left_pos]<=array[right_pos]:
                temp[temp_pos] = array[left_pos]
                left_pos += 1
            else:
                temp[temp_pos] = array[right_pos]
                right_pos += 1
            temp_pos += 1
        # 如果左序列还有剩余
        while left_pos<=left_end:
            temp[temp_pos] = array[left_pos]
            left_pos += 1
            temp_pos += 1
        # 如果右序列还有剩余
        while right_pos<=right_end:
            temp[temp_pos] = array[right_pos]
            right_pos += 1
            temp_pos += 1
        for temp_pos in range(left_start, right_end + 1):
            array[temp_pos] = temp[temp_pos]
            
    def m_sort(left, right):
        '''分割序列，递归进行排序'''
        if left>=right:
            return
        center = (left + right) // 2
        m_sort(left, center)
        m_sort(center+1, right)
        m_merge(left, center, right)
        
    if len(array)>=2:
        temp = [0] * len(array)
        m_sort(0,len(array)-1)

// C 实现
void Merge(ElemType *A, ElemType *Temp, int leftStart, int leftEnd, int rightEnd){
    /*将两个有序子序列合并*/
    int rightPos = leftEnd+1;
    int leftPos = leftStart;
    int tempPos = leftStart;
    while(leftPos<=leftEnd && rightPos<=rightEnd){
        if(A[leftPos]<=A[rightPos])
            Temp[tempPos++] = A[leftPos++];
        else
            Temp[tempPos++] = A[rightPos++];
    }
    // 如果左序列还有剩余
    while(leftPos<=leftEnd)
        Temp[tempPos++] = A[leftPos++];
    // 如果右边序列还有剩余
    while(rightPos<=rightEnd)
        Temp[tempPos++] = A[rightPos++];
    for(tempPos=leftStart;tempPos<=rightEnd;tempPos++)
        Temp[tempPos] = A[tempPos];
}

void MergeSortCore(ElemType *A, ElemType *Temp, int left, int right){
    /*分割序列，递归进行排序*/
    if(left<right){
        int center = (left+right)/2;
        MergeSortCore(A, left, center);
        MergeSortCore(A, center+1, right);
        Merge(A, Temp, left, center, right);
    }
}

void MergeSort(ElemType *A, int count){
    if(count>=2){
        Elemtype Temp[count];
        MergeSortCore(A, Temp, 0, count-1)
    }
}

// Java
@SuppressWarnings("unchecked")
public static <T extends Comparable<T>> void mergeSort(T[] arr){
    if (arr.length)>=2){
        T[] temp = (T[])new Comparable[arr.length];
        mergeSortCore(arr, temp, 0, arr.length-1);
    }
}

public static <T extends Comparable<T>> void mergeSortCore(T[] arr, T[] temp, int left, int right){
    if(left<right){
        int center = (left+right)/2;
        mergeSortCore(arr, temp, left, center);
        mergeSortCore(arr, temp, center+1, right);
        merge(arr, temp, left, center, right);
    }
}

public static <T extends Comparable<T>> void merge(T[] arr, T[] temp, int leftStart, int leftEnd, int rightEnd){
    int rightPos = leftEnd+1;
    int leftPos = leftStart;
    int tempPos = leftStart;
    while (leftPos<=leftEnd && rihgtPos<=rightEnd){
        if(arr[leftPos],compareTo(arr[rightPos])<=0)
            temp[tempPos++] = arr[leftPos++];
        else
            temp[tempPos++] = arr[rightPos++];
    }
    if (leftPos<=leftEnd)
        System.arraycopy(arr, leftPos, temp, tempPos, leftEnd+1-leftPos);
    if (rightPos<=rightEnd)
        System.arraycopy(arr, rightPos, temp, tempPos, rightEnd+1-rightPos);
    System.arraycopy(temp, leftStart, arr, leftStart, rightEnd+1-leftStart);
}

3.6 计数排序

3.6.1 特点

通过计数的方法，可实现无比较的排序，从而可以突破 nlogn 的最差时间复杂度限制，实现线性时间排序。

假设输入元素均为 [0, k] 区间的整数，对于每一个元素，确认小于它的元素个数，然后放回合适的位置。

3.6.2 实现

# Python 实现
# 假设元素均为在 [0,k] 区间的正整数
def counting_sort(array, k):
    counts = [0]*(k+1)
    new = [0]*len(array)
    for elem in array:
        # counts[elem] 为元素 elem 出现的次数
        counts[elem] += 1
    for elem in range(1,k+1):
        # counts[elem] 为小于等于元素 elem 的元素出现的次数
        counts[elem] = counts[elem] + counts[elem-1]
    # 输出有序序列
    for elem in array:
        new[count[elem]-1] = elem
        count[elem] -= 1
    # 赋值回原序列
    array[:] = new

// C 实现
// 假设元素均为在 [0,k] 区间的正整数
void CountingSort(int *A, int n, int k){
    int counts[k+1];
    int new[n];
    // counts[A[i]] 为元素 A[i] 出现的次数
    for(int i = 0; i<n; i++) counts[A[i]]++;
    for(int elem = 0; elem<=k; elem++){
        // counts[elem] 为小于等于元素 elem 的元素出现的次数
        counts[elem] = counts[elem] + counts[elem-1];
    }
    // 输出有序序列
    for(i = 0; i<n; i++){
        new[count[A[i]]-1]=A[i];
        count[A[i]]--;
    }
    // 赋值回原序列
    for(i = 0; i<n; i++){
        A[i] = new[i];
    }
}

3.6.3 时间复杂度：O(n+k)

平均时间复杂度：O(n+k)

最坏时间复杂度：O(n^2)

空间复杂度：O(n+k)

3.7 桶排序

3.7.1 特殊形式

在计数排序时，如果不追求排序的稳定性，当每个元素的出现的次数统计完毕后，就可以直接输出目标序列，此时简化后的计数排序就是桶排序的一种特殊情况。

# Python 实现
# 假设元素均在 [0,k] 区间

# 直接由计数排序转化的不稳定版本
def bucket_sort(array, k):
    counts = [0]*(k+1)
    for elem in array:
        # counts[elem] 为元素 elem 出现的次数
        counts[elem] += 1
    # 此时 array 中的数值已经无用，而 counts 中记录了所有数值出现的次数
    del array[:]
    for elem, count in enumerate(counts):
        for _ in range(count):
            array.append(elem)

# 优化以后的稳定版本，计数改为直接记录元素
def bucket_sort(array, k):
    buckets = [[] for i in range(k+1)]
    for elem in array:
        # buckets[elem] 记录了出现的所有 elem 元素
        buckets[elem].append(elem)
    # 此时 array 中的数值已经无用，而 buckets 中记录了所有的元素
    del array[:]
    for bucket in filter(None, buckets):
        array.extend(bucket)

// C 实现
// 假设元素均为在 [0,k] 区间的正整数
void BucketSort(int *A, int n, int k){
    int counts[k+1];
    // counts[A[i]] 为元素 A[i] 出现的次数
    for(int i = 0; i<n; i++) counts[A[i]]++;
    for(i = 0, elem = 0; elem<=k; elem++){
        for(int j=0; j<counts[elem]; j++){
            A[i++] = elem;
        }
    }
}

// 优化以后的稳定版本，计数改为直接记录元素
typedef float ElemType;
typedef struct ListNode{
    ElemType data;
    struct ListNode *next;
} ListNode, *LinkedList;

LinkedList NewList(){
    /*新建链表*/
    dummy = (ListNode *)malloc(sizeof(ListNode));
    if(!dummy) FatalError("Out of Space");
    dummy->next = NULL;
    return dummy;
}

void Insert(LinkedList p, ElemType key){
    /*链表插入*/
    node = (ListNode *)malloc(sizeof(ListNode));
    if(!node) FatalError("Out of Space");
    node->data = key;
    node->next = p->next;
    p->next = node;
}

void BucketSort(int *A, int n, int k){
    ListNode *buckets[n];
    // 初始化每个桶（链表）
    for(int i = 0; i<n; i++) buckets_tail[i] = buckets[i] = NewList();
    for(int i = 0; i<n; i++){
        // buckets[A[i]] 为出现的全部元素 A[i]
        Insert(buckets_tail[A[i]], A[i]);
        buckets_tail[A[i]] = buckets_tail[A[i]]->next; 
    }
    for(i = 0, elem = 0; elem<=k; elem++){
        // 倒出桶内数据，并释放桶
        while(buckets[elem]->next){
            A[i++] = buckets[elem]->next->data;
            temp = buckets[elem];
            buckets[elem] = buckets[elem]->next;
            free(temp);
        }
        free(buckets[elem]);
    }
}

3.7.2 一般形式

当不满足计数排序的条件时，需要对其进行散列化，每个桶中使用链表存储多个数值。其结构类似于哈希表。

# Python 实现
# 假设元素均匀分布在 [0,1) 区间
def bucket_sort(array):
    n = len(array)
    # 为了简洁这里没有使用链表，使用了二维 list
    buckets = [[] for i in range(n)]
    for elem in array:
        buckets[int(n*elem)].append(elem)
    del array[:]
    for bucket in filter(None, buckets):
        insertion_sort(bucket)
        array.extend(bucket)

// C 实现
// 假设元素均匀分布在 [0,1) 区间
typedef float ElemType;
typedef struct ListNode{
	ElemType data;
	struct ListNode *next;
} ListNode, *LinkedList;

LinkedList NewList(){
    /*新建链表*/
    dummy = (ListNode *)malloc(sizeof(ListNode));
    if(!dummy) FatalError("Out of Space");
    dummy->next = NULL;
    return dummy;
}

void Insert(LinkedList p, ElemType key){
    /*链表插入*/
    node = (ListNode *)malloc(sizeof(ListNode));
    if(!node) FatalError("Out of Space");
    node->data = key;
    node->next = p->next;
    p->next = node;
}

void BucketSort(ElemType *A, int n, int k){
    /* 桶排序 */
    ListNode *buckets[n];
    // 初始化每个桶（链表）
    for(int i = 0; i<n; i++) buckets[i] = NewList();
    int index;
    ListNode *p;
    for(j = 0; j<n; i++){
        // 分配桶
        index = (int)(n*A[j]);
        // 按顺序插入桶
        // p->next->data<=A[j] 中，“等于”时仍然后移，是为了维持稳定性
        for(p = buckets[index]; p->next && p->next->data<=A[j]; p = p->next){
            Insert(p, A[j]);
        }
    }
    // 按顺序回写到原序列，并释放桶
    for(i = 0, j = 0; i<n; i++){
        while(buckets[i]->next){
            A[j++] = buckets[i]->next->data;
            temp = buckets[i];
            buckets[i] = buckets[i]->next;
            free(temp);
        }
        free(buckets[i]);
    }
}

3.7.3 时间复杂度：O(n+k)

平均时间复杂度：O(n+k)

最坏时间复杂度：O(n^2)

空间复杂度：O(n+k)

3.8 基数排序

3.8.1 特点

基数排序适用于正整数排序。

首先将序列中所有的数字统一为相同位数（通过在前面补 0），然后逐位进行比较。

3.8.2 实现

def radix_sort(array, radix = 10):
    # 求最大位数 digit
    max_num = max(array)
    digit = 0
    while max_num>0:
        max_num //= radix
        digit += 1
    # 从最后一位起，以每一位为 key 进行桶排序(基数为几就是几个桶，每个桶里无需再排序）
    for i in range(1,digit):
        buckets = [[] for i in range(radix)]
        for elem in array:
        	buckets[elem%(radix**i)//(radix**(i-1))].append(elem)
        del array[:]
        for bucket in filter(None, buckets):
            array.extend(bucket)

// C 实现
// 假设元素均为正整数
typedef float ElemType;
typedef struct ListNode{
	ElemType data;
	struct ListNode *next;
} ListNode, *LinkedList;

LinkedList NewList(){
    /*新建链表*/
    dummy = (ListNode *)malloc(sizeof(ListNode));
    if(!dummy) FatalError("Out of Space");
    dummy->next = NULL;
    return dummy;
}

void Insert(LinkedList p, ElemType key){
    /*链表插入*/
    node = (ListNode *)malloc(sizeof(ListNode));
    if(!node) FatalError("Out of Space");
    node->data = key;
    node->next = p->next;
    p->next = node;
}

void DeleteList(LinkedList L){
    LinkedList P,temp;
    // 假设有头结点，P 初始指向头结点指向的结点
    P = L->next;
    // 清空头结点的指向
    L->next = NULL;
    // 从 P 开始逐个释放结点
    while(P){
        temp = P->next;
        free(P);
        P = temp;
    }
}

void RadixSort(ElemType *A, int n, int radix){
    ElemType max = A[0];
    LinkedList buckets[radix];
    // 初始化每个桶（链表）
    for(int i = 0; i<radix; i++) buckets[i] = NewList();
    // 寻找最大值
    for(i=0; i<n; i++) max = max>A[i]?max:A[i];
    int digit = 0;
    while(max>0){
        max /= radix;
        digit++;
    }
    // 从最后一位起，以每一位为 key 进行桶排序(基数为几就是几个桶，每个桶里无需再排序）
    for(int d = 1; d<digit; d++){
        for(i = 0; i<n; i++;){
            index = A[i]%pow(radix,d)/pow(radix,(d-1));
            for(p = buckets[index]; p->next && p->next->data<=A[i]; p = p->next){
                Insert(p, A[i]);
            }
        }
        // 按顺序回写到原序列，并释放桶
        for(i = 0, j = 0; i<n; i++){
            while(buckets[i]->next){
                A[j++] = buckets[i]->next->data;
                temp = buckets[i];
                buckets[i] = buckets[i]->next;
                free(temp);
            }
        }
    }
}

<推广> 本站使用 NameSilo 提供的域名服务。

第3章 排序算法

3.1 简单排序算法

3.1.1 冒泡排序

3.1.2 插入排序

3.1.3 选择排序

3.2 希尔排序

3.3 堆排序

3.3.1 时间复杂度：O(nlogn)

3.3.2 空间复杂度：O(1)

3.3.3 稳定性：不稳定

3.3.4 实现

3.4 快速排序

3.4.1 基准值的选择

1）不合适的取法

2）随机数法

3）三数取中法

3.4.2 非原地排序

3.4.3 原地分割策略

1）单向扫描

2）双向扫描

3.4.4 复杂度和稳定性

1）时间复杂度：O(nlogn)

2）稳定性：不稳定

3）空间复杂度

4）特别之处

3.4.5 优化

3.5 归并排序

3.5.1 时间复杂度：O(nlogn)

3.5.2 稳定性：稳定

3.5.3 空间复杂度：O(n)

3.5.4 实现

3.6 计数排序

3.6.1 特点

3.6.2 实现

3.6.3 时间复杂度：O(n+k)

3.7 桶排序

3.7.1 特殊形式

3.7.2 一般形式

3.7.3 时间复杂度：O(n+k)

3.8 基数排序

3.8.1 特点

3.8.2 实现

第3章排序算法