重新看了一段时间的数据结构和算法,写点总结和梳理。
使用 Python 和 C 语言进行描述。
第2章 树
2.1 基础知识
2.1.1 树
树(tree)是一种具有树状结构的数据结构,有若干子结点,有且只有一个根结点。
2.1.2 森林
多颗树构成森林。
森林可以转换为树。
2.1.3 应用
对于大量的数据,链表的线性访问时间太慢。而通过构建树,可以按照分层级别进行访问和操作,可以大幅提高效率。
一个常见的应用是后面将会提到的二叉查找树,在此之前,需要对二叉树有一定的了解。
2.1.4 实现
容易想到,在结点的结构中,存储指向子结点的指针,即可实现一棵树。
然而,对于一棵一般的树,每个结点的子结点的数目是未知的。所该方式无法用来实现一般的树。
解决的方法是,将所有的子结点放置于一个链表中,父节点中存储指向首个子结点的指针。
# Python 实现
class BiTNode:
def __init__(self, x):
self.data = x
self.first_child = None
self.next_sibling = None// C 实现
typedef struct BiTNode{
ElemType data;
struct BiTNode *FirstChild; *NextSibling;
} BiTNode,*BiTree;2.2 二叉树
二叉树(Binary tree)是每个结点最多有两个分支的树结构。
二叉树的分支具有左右次序,不能颠倒。
普通的树可以转换为二叉树。
2.2.1 性质
二叉树多第 i 层最多有 2^(i+1)个结点;
深度为 k 的二叉树最多有2^(k+1)-1 个结点(根结点 k = 0);
2.2.2 实现
# Python 实现
class BiTNode:
def __init__(self, x):
self.key = x
self.left = None
self.right = None
self.p = None// C 实现
typedef struct BiTNode{
ElemType key;
struct BiTNode *left, *right, *p;
} BiTNode,*BiTree;2.2.3 遍历
1)层序遍历
层数按照从上到下的层顺序访问。
# Python 实现
def level_order(node):
if !node:
return
nodes = dequeue([node])
while nodes:
node = popleft(nodes)
print(node.key)
if node.left:
nodes.append(node.left)
if node.right:
nodes.append(node.right)
# Python 递归实现
# 并没什么用
def level_order(*nodes):
children = []
for node in filter(None,nodes):
print(node.key)
children.append(node.left)
children.append(node.right)
if children:
level_order(*children)// C 实现
void visit(ElemType key){
/*Do sth.*/
}
void levelOrder(BiTree T){
LinkQueue nodes = InitQueue();
if(T) EnQueue(nodes, T);
BiTree node;
while(!IsEmpty(nodes)){
node = DeQueue(nodes)
visit(node->key);
if(node->left) EnQueue(nodes,node->left);
if(node->right) EnQueue(nodes,node->right);
}
}2)先序遍历
先(前)序,指的是先访问结点本身(结点本身即当前的根结点)。
遍历顺序:根结点N -> 左子树L -> 右子树R (NLR)
# Python 实现
def pre_order(node):
if node is not None:
print(node.key)
pre_order(node.left)
pre_order(node.right)// C 实现
void preOrder(BiTree T){
if(T){
visit(T->key);
preOrder(T->left);
preOrder(T->right);
}
}3)中序遍历
中序遍历,指的是结点本身在中间访问。
遍历顺序:左子树->根结点->右子树
# Python 实现
def in_order(node):
if node is not None:
in_order(node.left)
print(node.key)
in_order(node.right)4)后序遍历
后序遍历,指的是最后访问根结点。
遍历顺序:左子树->右子树->根结点
# Python 实现
def post_order(node):
if node is not None:
post_order(node.left)
post_order(node.right)
print(node.key)2.2.4 特殊形态
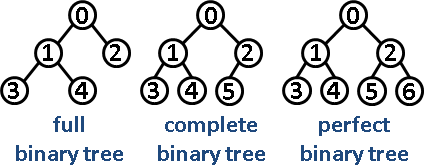
1)完全二叉树
完全二叉树(Complete binary tree)每层结点都完全填满,在最后一层上如果不是满的,则只缺少右边的若干结点。
当右边无缺失时,即成为完美二叉树。
通常使用数组来实现完全二叉树,因其可以以层序遍历的方式放入一个数组中,从而快速定位到其中的某个结点。
2)完美二叉树、满二叉树
s q完美二叉树(Perfect binary tree)每层结点都完全填满。所有非叶子结点都有两个孩子,所有叶子结点都在同一层。
国内定义的满二叉树(严蔚敏),即为完美二叉树。国外定义的满二叉树(Full binary tree):每个结点有零个或两个孩子,不存在只有一个孩子的结点。
2.3 二叉搜索树
二叉搜索树/二叉查找树/排序二叉树(Binary Search Tree,BST),是树的一个核心应用。
在二叉搜索树中,对于每个节点,左孩子值都小于结点值,结点值都小于右孩子值。
2.3.1 特点
左子树的所有结点 < 父结点 < 右子树的所有结点,中序遍历可使结点有序。
使用二叉搜索树的原因:
大部分操作(如查找、插入、删除)的平均时间复杂度只有 O(logn),可以同时保证查找效率和插入效率。
2.3.2 查找
从父结点开始查找:若小于父结点,递归查找左子树;若大于父结点,递归查找右子树。
当等于父结点或者父节点为空时,完成查找,返回父结点。
2.3.3 插入
从父结点开始插入:若小于父结点,递归插入左子树;若大于父结点,递归插入右子树。
当父节点为空时,则新建结点作为父结点,完成插入。
2.3.4 删除
1) 结点为叶子结点
直接删除。此情况可并入情况2中。
2)结点有一个子结点
删除后用其子结点取代它的位置。
3)结点有两个子结点
因二叉搜索树的定义,易知,可从左子树取来最大结点,或者从右子树取来最小结点。
一般寻找右子树的最小结点 m,将其数值赋给当前结点 p,然后递归删除最小结点 m。
因为最小结点一定没有左子树,因此删除该结点属于情况1、2。
2.3.3 实现
# Python 实现
class BSTreeNode:
def __init__(self, val):
'''定义结点'''
self.key = val
self.left = None
self.right = None
self.p = None
def search(self, val):
'''从当前结点开始查找值为 val 的结点'''
while self and self.key != val:
if self.key<val:
self = self.left
else self = self.right
return self
def minimum(self):
'''从当前结点开始查找最小的结点'''
while self.left:
self = self.left
return self
def maximum(self):
'''从当前结点开始查找最大的结点'''
while self.right:
self = self.right
return self
def successor(self):
'''查找后继'''
if self.right:
return self.right.minimum()
parent = self.p
while parent and self is parent.right:
self = parent
parent = parent.p
return parent
def presuccessor(self):
'''查找前驱'''
if self.left:
return self.right.maximum()
parent = self.p
while parent and self is parent.left:
self = parent
parent = parent.p
return parent
class BSTree:
def __init__(self):
'''树定义'''
self.root = None
def insert(self, node):
'''插入结点'''
parent = None
cur = self.root
while cur:
parent = cur
if node.key < cur.key:
cur = cur.left
else:
cur = cur.right
node.p = parent
if parent is None:
self.root = node
elif node.key < parent.key:
parent.left = node
else:
parent.right = node
def transplant(self, target, node):
'''迁移结点'''
if target.p is None:
self.root = node
elif target is target.p.left:
target.p.left = node
else:
target.p.right = node
if node:
node.p = target.p
def delete(self, node):
'''删除结点'''
# 无孩子或者只有一个孩子,直接用孩子取代待删除结点
if node.left is None:
self.transplant(node, node.right)
elif node.right is None:
self.transplant(node, node.left)
else:
# 两个孩子,用右子树的最小结点(及其子树)取代待删除结点
temp = node.right.mininum()
# 若 node 与 temp 之间还有结点
if temp.p is not node:
# 用 temp 的右子树取代 temp 的位置,取出 temp,然后将 node 的右子树作为 temp 的右子树
self.transplant(temp, temp.right)
temp.right = node.right
temp.right.p = temp
# 用 temp(及其子树)取代 node
self.transplant(node, temp)
temp.left = node.left
temp.left.p = temp// C 实现
typedef struct BSTreeNode{
ElemType key;
struct BSTreeNode *left, *right, *p;
} BSTreeNode;
typedef struct BSTree{
struct BSTreeNode *root;
} *BSTree;
/* 从结点 node 开始查找值为 val 的结点 */
BSTreeNode* Search(BSTreeNode* node, ElemType val){
while(node && (node->key != val)){
node = (node->key < val)? node->left : node->right;
}
return node;
}
/* 从结点 node 开始查找最小的结点 */
BSTreeNode* Minimum(BSTreeNode* node){
if(node){
while(node->left) {node = node->left;}
}
return node;
}
/* 从结点 node 开始查找最大的结点 */
BSTreeNode* Maximum(BSTreeNode* node){
if(node){
while(node->right) {node = node->right;}
}
return node;
}
/* 查找后继 */
BSTreeNode* Successor(BSTreeNode* node){
BSTreeNode* parent = NULL;
if(node){
if(node->right) return Minimum(node->right);
parent = node->p;
while(parent && node==parent->right){
node = parent;
parent = parent->p;
}
}
return parent;
}
/* 查找前驱 */
BSTreeNode* Presuccessor(BSTreeNode* node){
BSTreeNode* parent = NULL;
if(node){
if(node->right) return Maximum(node->left);
parent = node->p;
while(parent && node==parent->left){
node = parent;
parent = parent->p;
}
}
return parent;
}
/* 插入结点 */
void Insert(BSTree T, BSTreeNode* node){
if(!T || !node) Error("Null Pointer");
BSTreeNode* parent = NULL;
BSTreeNode* cur = T->root;
while(cur){
parent = cur;
cur = (node->key < cur->key) ? cur->left : cur->right;
}
node->p = parent;
if(!parent) T->root = node;
else if(node->key < parent->key) parent->left = node;
else parent->right = node;
}
/* 迁移结点 */
void Transplant(BSTree T, BSTreeNode* target, BSTreeNode* node){
if(!T || !node) Error("Null Pointer");
if(!target->p) T->root = node;
else if(target == target->p->left) target->p->left = node;
else target->p->right = node;
if(node) node->p = target->p;
}
/* 删除结点 */
void Delete(BSTree T, BSTreeNode *node){
if(!T || !node) Error("Null Pointer");
//无孩子或者只有一个孩子,直接用孩子取代待删除结点
if(!node->left) Transplant(T, node, node->right);
else if(!node->right) Transplant(T, node, node->left);
else{
//两个孩子,用右子树的最小结点(及其子树)取代待删除结点
BSTreeNode *temp = Minimum(node->right);
//若 node 与 temp 之间还有结点
if(temp->p != node){
//用 temp 的右子树取代 temp 的位置,取出 temp,然后将 node 的右子树作为 temp 的右子树
Transplant(temp, temp->right);
temp->right = node->right;
temp->right->p = temp;
}
//用 temp(及其子树)取代 node
Transplant(node, temp);
temp->left = node->left;
temp->left->p = temp;
}
free(node);
}2.3.3 缺点
当二叉查找树中,当进行大量的插入、删除操作之后,或者插入一个总体有序的序列,会导致其左右失衡,深度超出预期;最极端的情况即成为链表。
可以通过施加平衡条件,或者在每次操作后施加规则进行调整来解决该问题。
2.4 AVL 树
2.4.1 特点
AVL 树是最早的自平衡二叉查找树。
AVL 树是每个节点左子树和右子树高度(空树的高度为 -1)最多差 1 的二叉查找树。
2.4.2 时间复杂度
查找、插入、删除的平均和最坏时间复杂度都是 O(log n)
2.4.3 旋转
易知,对 AVL 树进行插入/删除操作时,可能会破坏 AVL 树的平衡条件。
此时需要通过一次或多次旋转来重新平衡这棵树。
# Python 实现
class BSTNode:
def __init__(self, val):
self.data = val
self.left = None
self.right = None
self.p = None
class AVLTree:
def __init__(self):
# 为处理边界条件,使用一个游标 self.nil 来代表 NIL 结点
self.nil = BSTNode(0)
self.root = None
def left_rotate(self, node):
# 假设根结点的父结点为 self.nil
if node.right is self.nil:
raise ValueError("Nil Node")
temp = node.right
# temp 的左孩子 成为 node 的右孩子
node.right = temp.left
if temp.left != self.nil:
temp.left.p = node
# 更新 temp 的父亲,若父亲不为 NIL,还要更新父亲的子结点信息
temp.p = node.p
if node.p == self.nil:
self.root = temp
elif node == node.p.left:
node.p.left = temp
else:
node.p.right = temp
# node 成为 temp 的左孩子
temp.left = node
node.p = temp
def right_rotate(self, node):
if node.left is self.nil:
raise ValueError("Nil Node")
temp = node.left
node.left = temp.right
if temp.right != self.nil:
temp.right.p = node
temp.p = node.p
if node.p == self.nil:
self.root = temp
elif node == node.p.left:
node.p.left = temp
else:
node.p.right = temp
temp.right = node
node.p = temp
// C 实现
typedef struct BSTreeNode{
ElemType key;
struct BSTreeNode *left, *right, *p;
} BSTreeNode;
typedef struct BSTree{
struct BSTreeNode *root;
} *BSTree;
BSTreeNode *BSTreeNil = (BSTreeNode *)malloc(sizeof(BSTreeNode));
void LeftRotate(BSTree T, BSTreeNode node){
// 假设根结点的父结点为 BSTreeNil
if(!T || !node || node->right) Error("Null Pointer");
if(node->right == BSTreeNil) Error("NIL Node");
BSTreeNode temp = node->right;
// temp 的左孩子成为 node 的右孩子
node->right = temp->left;
if(temp->left != BSTreeNil)
temp->left->p = node;
// 更新 temp 的父亲
temp->p = node->p;
if(node->p == BSTreeNil)
T->root = temp;
else if(node==node->p->left)
node->p->left = temp;
else node->p->right = temp;
temp->left = node;
node->p = temp;
}
void RightRotate(BSTree T, BSTreeNode node){
// 假设根结点的父结点为 BSTreeNil
if(!T || !node || node->left) Error("Null Pointer");
if(node->left == BSTreeNil) Error("NIL Node");
BSTreeNode temp = node->left;
node->left = temp->right;
if(temp->right != BSTreeNil)
temp->right->p = node;
temp->p = node->p;
if(node->p == BSTreeNil)
T->root = temp;
else if(node==node->p->left)
node->p->left = temp;
else node->p->right = temp;
temp->right = node;
node->p = temp;
}1)单旋转
左左:
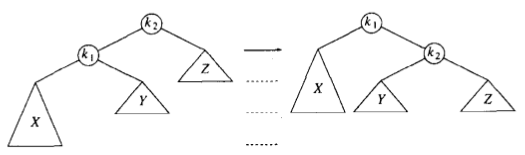
右右:
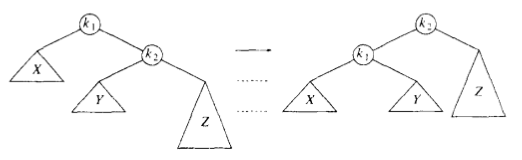
2)双旋转
对于左右、右左的情况,单旋转无法修复平衡:
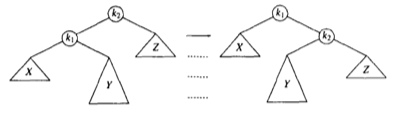
对此可以通过两次单旋转解决(左旋+右旋/右旋+左旋)
2.4.4 插入
对于结点 T,插入新结点时,有四种情况会导致平衡被破坏:
1、对 T 的左儿子的左子树进行插入(左左)
2、对 T 的右儿子对右子树进行插入(右右)
3、对 T 的左儿子的右子树进行插入(左右)
4、对 T 的右儿子的左子树进行插入(右左)
2.4.5 删除
略。
2.5 红黑树
2.5.1 特点
红黑树给二叉搜索树的结点加入两种颜色信息,通过对颜色的限制,保证没有一条路径会比其他路径长两倍,从而近似于平衡。
红黑树并不要求完全平衡,所以减少了旋转的次数,从而具有比 AVL 树更好的统计性能。
红黑树性质如下:
1、每个结点非黑即红;
2、根结点为黑色
3、叶子(NIL)结点为黑色
4、对于任一红色结点,它的子结点均为黑色
5、对于任意结点,从结点到它所有后代的简单路径上,包含相同数目的黑色结点
2.5.2 时间复杂度
查找、插入、删除的平均和最坏时间复杂度都是 O(log n)
2.5.3 旋转
易知,对红黑树进行插入/删除操作时,可能会破坏红黑树的平衡条件。
此时需要通过最多三次旋转来重新平衡这棵树。
红黑树的旋转同 AVL 树。
2.5.4 插入
当插入新结点时,通常用它取代树的一个 NIL 结点。
若新结点为黑色,则一定不满足最后一个性质。故新结点应为红色。
插入新结点 node 之后,若父结点为黑色,则无需调整;
若父结点为红色,且为左儿子则有以下几种情况:
1)叔结点为红色
染黑父结点、叔结点,染红祖父结点;
因为祖父结点被染红,使祖父结点成为当前结点,并继续判断当前结点。
2)叔结点为黑色
【父结点为左孩子】
若当前结点为右孩子,则父结点成为当前结点,对当前结点左旋,当前结点成为左孩子。
染黑父结点,染红祖父结点,对祖父结点右旋。
【父结点为右孩子】
则与左孩子情况旋转方向相反。
2.5.5 删除
红黑树的删除操作核心部分同二叉搜索树。
使用二叉搜索树的删除操作,从红黑数中删除结点时,有以下两种情况:
1)结点有少于两个非 NIL 子结点
移走结点时,若它为黑色,则可能破坏红黑树性质。
2)结点有两个非 NIL 子节点
结点被其后继替代时,因为后继结点已经与其子节点分离,所以只要更改后继结点的颜色,就可以保持红黑树的性质;
但是其后继节点与子节点分离的过程,即移走该后继节点时,若它为黑色,则可能破坏红黑数的性质。
1)2)综上
用变量 temp 来跟踪这个被移走的结点,用 temp_original_color 来表示该结点原本的颜色,对于情况1,temp 为结点本身;对于情况2, temp 为结点的后继;
用变量 child 来跟踪 temp 的非 NIL 子结点,child 就是移植到 temp 的结点。另因为红黑树的 NIL 结点也需要染色,故 child 即使是 NIL 结点,也应当保存父结点的索引。
以 child 结点为索引,进行 fixup 操作,恢复红黑树性质。
2.5.6 实现
# Python 实现
class RBTreeNode:
def __init__(self, val):
self.data = val
self.left = None
self.right = None
self.p = None
self.color = 'black'
class RBTree:
def __init__(self):
# 为处理边界条件,使用一个游标 self.nil 来代表 NIL 结点
self.nil = RBTreeNode(0)
self.root = None
def left_rotate(self, node):
# 假设根结点的父结点为 self.nil
if node.right is self.nil:
raise ValueError("Nil Node")
temp = node.right
# temp 的左孩子成为 node 的右孩子
node.right = temp.left
if temp.left != self.nil:
temp.left.p = node
# 更新 temp 的父亲,若父亲不为 NIL,还要更新父亲的子结点信息
temp.p = node.p
if node.p == self.nil:
self.root = temp
elif node == node.p.left:
node.p.left = temp
else:
node.p.right = temp
# node 成为 temp 的左孩子
temp.left = node
node.p = temp
def right_rotate(self, node):
if node.left is self.nil:
raise ValueError("Nil Node")
temp = node.left
node.left = temp.right
if temp.right != self.nil:
temp.right.p = node
temp.p = node.p
if node.p == self.nil:
self.root = temp
elif node == node.p.left:
node.p.left = temp
else:
node.p.right = temp
temp.right = node
node.p = temp
def insert(self, node):
parent = self.nil
cur = self.root
while cur:
parent = cur
cur = cur.left if node.key < cur.key else cur.right
node.p = parent
if parent is self.nil:
self.root = node
elif node.key < parent.key:
parent.left = node
else:
parent.right = node
node.left = node.right = self.nil
node.color = 'red'
self.insert_fixup(node)
def insert_fixup(self, node):
# 直到当前结点(红色)的父亲为黑色为止
while node.p.color == 'red':
if node.p is node.p.p.left:
uncle = node.p.p.right
# 【情况 1】叔结点为红色
# 则染黑父结点、叔结点,染红祖父结点
if uncle.color == 'red':
node.p.color = uncle.color = 'black'
node.p.p.color = 'red'
# 祖父结点成为新的当前结点 node,满足【情况 2/3】
node = node.p.p
else:
# 【情况 2】叔结点为黑色,但是 node 为父结点的右孩子
# 父结点成为当前结点(node),对 node 左旋,node 成为父结点的左孩子,满足【情况3】
if node is node.p.right:
node = node.p
self.left_rotate(node)
# 【情况 3】叔结点为黑色,node 为父结点的左孩子
# 染黑父结点,染红祖父结点,对祖父结点右旋
node.p.color = 'black'
node.p.p.color = 'red'
self.right_rotate(node.p.p)
else:
uncle = node.p.p.right
if uncle.color == 'red':
node.p.color = uncle.color = 'black'
node.p.p.color = 'red'
node = node.p.p
else:
if node is node.p.right:
node = node.p
self.right_rotate(node)
node.p.color = 'black'
node.p.p.color = 'red'
self.left_rotate(node.p.p)
self.root.color = 'black'
def transplant(self, target, node):
'''迁移结点'''
if target.p is self.nil:
self.root = node
elif target is target.p.left:
target.p.left = node
else:
target.p.right = node
# 不需要加 「if node is not self.nil:」 这个判断,因为后面 fixup 的时候会用得上父结点信息
node.p = target.p
def delete(self, node):
'''删除结点'''
temp = node
temp_original_color = temp.color
# 无孩子或者只有一个孩子,直接用孩子取代待删除结点
if node.left is self.nil:
child = node.right
self.transplant(node, node.right)
elif node.right is self.nil:
child = node.left
self.transplant(node, node.left)
else:
# 两个孩子,用右子树的最小结点(及其子树)取代待删除结点
temp = node.right.mininum()
temp_original_color = temp.color
child = temp.right
# 若 node 与 temp 之间还有结点
if temp.p is node:
# 这步操作针对的是 child 为 NIL 结点的情况,保证当 child 为 NIL 时,也能完成 fixup
child.p = temp
else:
# 用 temp 的右子树取代 temp 的位置,取出 temp,然后将 node 的右子树作为 temp 的右子树
self.transplant(temp, temp.right)
temp.right = node.right
temp.right.p = temp
# 用 temp(及其子树)取代 node
self.transplant(node, temp)
temp.left = node.left
temp.left.p = temp
temp.color = node.color
if temp_original_color == 'black':
self.delete_fixup(child)
def delete_fixup(self, node):
while node != self.root and node.color == 'black':
if node is node.p.left:
uncle = node.p.right
if uncle.color == 'red':
uncle.color = 'black'
node.p.color = 'red'
self.left_rotate(self, node.p)
uncle = node.p.right
if uncle.left.color == 'black' and uncle.right.color == 'black':
uncle.color = 'red'
node = node.p
else:
if uncle.right.color == 'black':
uncle.left.color = 'black'
uncle.color = 'red'
self.right_rotate(self, uncle)
uncle = node.p.right
uncle.color = node.p.color
node.p.color = 'black'
self.left_rotate(self, node.p)
node = self.root
else:
uncle = node.p.left
if uncle.color == 'red':
uncle.color = 'black'
node.p.color = 'red'
self.right_rotate(self, node.p)
uncle = node.p.left
if uncle.left.color =='black' and uncle.right.color == 'black':
uncle.color = 'red'
node = node.p
else:
if uncle.left.color == 'black':
uncle.right.color = 'black'
uncle.color = 'red'
self.left_rotate(self, uncle)
uncle = node.p.left
uncle.color = node.p.color
node.p.color = 'black'
self.right_rotate(self, node.p)
node = self.root
node.color = 'black'
2.6 最优二叉树/哈夫曼树
2.7 B 树
<推广> 本站使用 NameSilo 提供的域名服务。