重新看了一段时间的数据结构和算法，写点总结和梳理。

使用 Python 和 C/C++ 进行描述。

第1章线性表、栈、队列

1.1 线性表

  <script src="https://asciinema.org/a/laozhu/L479wueo.js" id="asciicast-laozhu/L479wueo" data-t="html,css,result"  data-size="small" data-theme="asciinema"     data-preload="1" async></script>

线性表（Linear List）是由多个 Data Element 组成的有限序列。

典型的实现方式包括顺序表、链表（Linked list）。

1.1.1 顺序表

分配连续的内存，使用连续的内存依次存储每个结点。

实现方式：数组/直接分配内存

查找结点的时间复杂度：O(1)

插入、删除结点的时间复杂度：O(n)

# Python 实现
# 直接使用列表 list
# 或者直接使用 array.array

// C 实现
// 直接使用数组

// 或者连续分配内存（动态数组）
const int LIST_INIT_SIZE 80
const int LIST_INCREMENT 80
typedef struct SqList{
    ElemType *elem;
    int length;
    int listsize;
}SqList;

// Init
void SqListInit(SqList *L){
    L->elem = (ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));
    if(!L->elem) FatalError("Null Pointer");
    L->length = 0;
    L->listsize = LIST_INIT_SIZE;
}

// Get
ElemType SqListGet(const SqList *L, int i){
    if(!L) FatalError("Null Pointer");
    if(i<0||i>=L.length) FatalError("Overflow");
    return *(L->elem+i);
}

void SqListIncrease(SqList *L){
    ElemType temp = realloc(
        L->elem, (L->listsize + LIST_INCREMENT)*sizeof(ElemType));
    if(!temp) FatalError("Overflow");
    L->elem = temp;
    L->listsize += LIST_INCREMENT;
}

// Pop
ElemType SqListPop(SqList *L){
    if(!L) FatalError("Null Pointer");
    if(L->length==0) FatalError("Underflow");
    L->length--;
    return *(L->elem + L->length);
}

// Append
void SqListAppend(SqList *L, ElemType val){
    if(!L) FatalError("Null Pointer");
    if(L->length==L->listsize) SqListIncrease(L);
    *(L->elem + L->length) = val;
    L->length++;
}

// Insert
void SqListInsert(SqList *L, int i, ElemType val){
    if(!L) FatalError("Null Pointer");
    if(L->length==L->listsize) SqListIncrease(L);
    for(ElemType *p = L->elem+L->length; p>i; p--){
      *p = *(p-1);
    }
    *p = val;
    L->length++;
}

// Delete
void SqListDelete(SqList *L, int i){
    if(!L) FatalError("Null Pointer");
    if(i<0||i>=L->length) FatalError("Overflow");
    L->length--;
    for(ElemType *p = L->elem+i; p < elem+L->length; p++){
        *p = *(p+1);
    }
}

// C++ 实现
// 直接使用静态数组
// 或者直接使用 vector

// 或者使用动态数组
const static size_t LIST_INIT_SIZE = 80;
const static size_t LIST_INCREMENT = 80;

template <typename T>
class SqList{
public:
    SqList(size_t size = LIST_INIT_SIZE)
    :_listsize(size), _length(0) {
        if(size<0) throw "Underflow";
        _elem = new T[size];
    }
    ~SqList(){delete [] _elem;}
    T& operator[](size_t pos) {return _elem[pos];}
    const T& operator[](size_t pos) const {return _elem[pos];}
    T& at(size_t pos);
    const T& at(size_t pos) const;
    T pop_back();
    size_t size() const {return _length;}
    size_t capacity() const {return _listsize;}
    void push_back(T item);
    void insert(size_t i, T item);
    void erase(size_t i);
    void clear();
private:
    T *_elem;
    size_t _length;
    size_t _listsize;
    void _increase(size_t size=LIST_INCREMENT);
};

// _increase
template <typename T>
void SqList<T>::_increase(size_t size){
    int newsize = _listsize + size;
    T *temp = new T[newsize];
    for(size_t i=0;i<_length;i++) temp[i]=_elem[i];
    delete [] _elem;
    _elem = temp;
    _listsize = newsize;
}

// at
template <typename T>
T& SqList<T>::at(size_t pos){
    if(pos<0||pos>=_length) throw "Overflow";
    return _elem[pos];
}
template <typename T>
const T& SqList<T>::at(size_t pos) const{
    if(pos<0||pos>=_length) throw "Overflow";
    return _elem[pos];
}

// pop_back
template<typename T>
T SqList<T>::pop_back(){
    if(_length==0) throw "Underflow";
    _length--;
    return _elem[_length];
}

// push_back
template <typename T>
void SqList<T>::push_back(T item){
    if(_length==_listsize) _increase();
    _elem[_length] = item;
    _length++;
}

// insert
template <typename T>
void SqList<T>::insert(size_t i, T item){
    if(i<0||i>_length) throw "Overflow";
    if(_length==_listsize) _increase();
    for(size_t j = _length;j>i;j--){
        _elem[j] = _elem[j-1];
    }
    _elem[i] = item;
    _length++;
}

// erase
template <typename T> 
void SqList<T>::erase(size_t pos){
    if(pos<0||pos>=_length) throw "Overflow";
    _length--;
    for(size_t j=pos; j<_length; j++){
        _elem[j]=_elem[j+1];
    }
}

// clear
template <typename T> 
void SqList<T>::clear(){
    T *temp = new T[LIST_INIT_SIZE];
    delete [] _elem;
    _elem = temp;
    _length = 0;
    _listsize = LIST_INIT_SIZE;
}

// Java 实现
// 直接使用数组 Array
// 或者直接使用数组列表 ArrayList

1.1.2 链表

不预先分配所有内存，在 Data Element 里定义指向下一个结点的指针，从而使用链式结构存储数据。

查找结点的时间复杂度：O(n)

插入、删除结点的时间复杂度：O(1)

1）头指针和头节点

链表一定有头指针，它就是一个普通指针，用来表示/指向一个链表，总是指向第一个结点

有头结点（表头）时候，头结点是第一个结点

没有头结点的时候，第一个元素就是第一个结点

2）单向链表

单向的链表就是单向链表（单链表）。Data Element 中包含结点的数据，与指向下个结点的指针。

# Python 实现
class LinkedList:
    class Node:
        def __init__(self, data=0, next_node=None):
            self.data = data
            self.next = next_node
            
        def insert(self, key):
            ''' 在当前结点后后插入 key '''
            self.next = Node(data, self.next)
            
        def delete_next(self):
    	    ''' 删除当前结点的后继结点 '''
    	    if self.next:
        	    self.next = self.next.next
            
    def __init__(self):
        self.head = None
    
    def search(self, key):
        node = self.head
        while node:
            node = node.next
        return node
    
    def insert(self, key):
        self.head = self.Node(key, self.head)
        
	def delete(self, key):
    	''' 删除第一个值为 key 的结点 '''
        prev = None
        node = self.head
        if not node: return
        if node.data == key:
            self.head = node.next
    	while node and node.data!=key:
        	prev = node
            node = node.next
        if node:
            prev.next = node.next
            
    def clear(self):
        self.head = self.Node()

// C 实现
typedef struct ListNode{
	ElemType data;
	struct ListNode *next;
} ListNode;

typedef struct LinkedList{
    ListNode *head;
} LinkedList;

LinkedList* LinkedListInit(){
    /* 新建一个链表 */
    LinkedList L = (LinkedList*)malloc(sizeof(LinkedList));
    if(NULL==L) FatalError("Out of Space");
    L->head = (ListNode*)malloc(sizeof(ListNode));
    if(NULL==L->head) FatalError("Out of Space");
    head->next = NULL;
    return L;
}

ListNode* LinkedListSearch(LinkedList* L, ElemType val){
    /* 在链表 L 中找到第一个值为 key 的结点 */
    ListNode* pnode = L->head;
    while(pnode && pnode->data!=val)
      pnode = pnode->next;
    return pnode;
}

ListNode* _LinkedListSearchPrev(LinkedList* L, ElemType val){
  /* 在链表 L 中找到第一个值为 key 的结点的前驱结点 */
  ListNode* pre = NULL;
  ListNode* pnode = L->head;
  while(node && node->data!=val){
    pre = pnode;
    pnode = pnode->next;
  }
  return NULL==pnode?pnode:pre;
}

void LinkedListInsertAfter(LinkedList p, ElemType key){
  /* 在 p 结点后插入一个结点，值为 key */
  if(NULL==p) FatalError("Null Pointer");
  node = (LinkedList)malloc(sizeof(ListNode));
  if(NULL==node) FatalError("Out of Space");
  node->data = key;
  node->next = p->next;
  p->next = node;
}

void LinkedListDeleteNext(LinkedList pre){
  /* 删除 pre 结点的后继结点 */
  if(pre && pre->next){
    temp = pre->next;
    pre->next = temp->next;
    free(temp);
  }
}

void LinkedListDeleteElem(LinkedList L, ElemType key){
  /* 删除第一个值为 key 的结点 */
  // 此处假设链表有头结点。否则需要先判断第一个结点，同时函数需要返回值
  pre = _LinkedListSearchPrev(L, key);
  DeleteNext(pre);
}

void LinkedListClear(LinkedList L){
  LinkedList P,temp;
  // 假设有头结点，P 初始指向头结点指向的结点
  P = L->next;
  // 清空头结点的指向
  L->next = NULL;
  // 从 P 开始逐个释放结点
  while(P){
    temp = P->next;
    free(P);
    P = temp;
  }
}

// C++ 实现
template <typename T>
class ListNode{
public:
    ListNode(ElemType val=0, ListNode* nextNode=0)
        :data(val),next(nextNode){};
    ~ListNode(){};
    ElemType data;
    ListNode *next;
};

template <typename ElemType>
class LinkedList{
public:
    LinkedList(){head = nullptr;};
    ~LinkedList(){clear();};
    ListNode *head;
    ListNode& search(const ElemType &val) const;
    void insert_node(const ListNode &node);
    void insert(const ElemType &val);
    void remove(ElemType val);
    void clear();
};

//Search
template <typename ElemType>
ListNode<ElemType>&
LinkedList<ElemType>::search(const ElemType &val) const{
    ListNode<ElemType> p = head;
    while(p && p->data!=val)
        p = p->next;
    return *p;
}

//Insert ListNode
template <typename ElemType>
void LinkedList<ElemType>::insert_node(const ListNode &node){
    ListNode<ElemType>* p = head;
    head = &node;
    node.next = p;
}

//Insert
template <typename ElemType>
void LinkedList<ElemType>::insert(const ElemType &val){
    head = new ListNode<ElemType>(val,head);
}


//Clear
template <typename ElemType>
void LinkedList<ElemType>::clear(LinkedList L){
  ListNode<ElemType>* p, temp;
  p = L->head;
  // 清空头结点的指向
  L->head = nullptr;
  // 从 p 开始逐个释放结点
  while(p){
    temp = p->next;
    delete p;
    p = temp;
  }
}

// Java 实现
public class SingleLinkedList<E>{
    private static class Node<E>{
        E item;
        Node<E> next;
        Node(E element, Node next){
            this.item = element;
            this.next = next;
        }
    }
    Node first = null;
    Node last = null;
    public boolean add(E e){
        Node<E> newNode = new Node<>(e,null);
        if(last!=null){
            last.next = newNode;
            last = last.next;
        }
        else{
            first = last = newNode;
        }
        return true;
    }
    public E get(int index){
        Node cur = first;
        for(int i=0;i<index;i++){
            cur = cur.next;
        }
        return (E)cur.item;
    }
}

3）双向链表

Data Element 中，除了指向下个结点的指针，还有指向上个结点的指针。

# Python 实现
class ListNode:
	def __init__(self, x):
		self.data = x
		self.next = None
		self.prev = None

// C 实现
typedef struct ListNode{
	ElemType data;
	struct ListNode *next;
	struct ListNode *prev;
} ListNode,*DualLinkedList;

// C++ 实现
// 直接使用 list 容器

// Java 实现
// 直接使用 LinkedList 类

4）循环链表

结构同单向链表/双向链表，但最后一个结点指向头结点，形成一个环。

【例】约瑟夫环

n 个人站成一个圆，从一个人开始数，每次数到 k 则杀一人，最终剩下的一人可存活。已知 n、k，求存活者的初始位置。

解法：

创建一个循环列表，直接模拟整个过程。

可使用递推的方式简化。

【例】判断链表是否有环

一个单向链表，判断其中是否有环。（尾指针指向其中某个结点即为有环）

解法：

使用两个指针从头结点开始遍历，p 每次走一个结点，q 每次走两个结点。

若某一刻 p 或 q 为 None，则无环；

若某一个 p==q，则有环。

5）静态链表

在不使用指针的情况下，实现链式存储。结点存储在数组中，每个结点包含数据和下一个结点的数组下标（游标）。

# Python 实现
# Data Element 同单链表，但 self.next 为整型
# 使用 list 存储 Data Element
# 没什么用
class ListNode:
	def __init__(self, x):
		self.data = x
		self.next = 0

// C 实现
// 也没什么用
typedef struct ListNode{
    ElemType data;
    int cur;	//为0时表示无指向
} ListNode, StaticLinkList[MAXSIZE];

1.2 栈

1.2.1 特点

栈（Stack），又译堆栈/堆叠。与堆（Heap）无关联。

只允许在一端（栈顶，top）输入和输出数据。

栈可以使用任意线性表实现。

1.2.2 数组实现（通常使用该方式）

// C 实现
typedef struct Stack {
  ElemType val[MAXSIZE];
  int top;	//也可直接存到 val[0]
} *Stack;

Stack NewStack(){
  Stack S = (Stack)malloc(sizeof(struct Stack));
  if(!S) FatalError("Out of Space");
  S->top = 0
  return S;
}

bool StackEmpty(Stack S){
  return S->top==0;
}

void Push(Stack S, ElemType x){
  if(S->top == MAXSIZE) Error("Overflow");
  S->val[++S->top]=x;
}

ElemType Pop(Stack S){
  if(StackEmpty(S)) Error("Underflow");
  return S->val[S->top--];
}

# Python 实现
# 直接使用 list，然后直接使用 list 的 append/push 等操作即可

1.2.3 链表实现（链栈）

直接使用单链表实现即可，在头指针处压栈/出栈。

# Python 实现
class LinkedStack:
	def __init__(self, val=0, next_node=None):
		self.data = val
		self.next = next_node
        
    def is_empty(self):
        return bool(self.next)
    
    def push(self,x):
        self.next = LinkedStack(x, self.next)
        
    def pop(self):
        node = self.next
        if node:
            val = node.data
            self.next = node.next
            return val

// C 实现
typedef struct ListNode{
  ElemType data;
  struct ListNode *next;
} ListNode, *LinkedStack;

LinkedStack NewStack(){
  /* 新建一个有表头的链表 */
  LinkedStack dummy = (ListNode *)malloc(sizeof(ListNode));
  if(!dummy) FatalError("Out of Space");
  dummy->next = NULL;
  return dummy;
}

bool StackEmpty(LinkedStack S){
  return S->next;
}

void Push(LinkedStack S, ElemType x){
  if(!S) FatalError("Null Pointer");
  LinkedStack node = (ListNode *)malloc(sizeof(ListNode));
  if(!node) FatalError("Out of Space");
  node->data = x;
  node->next = S->next;
  S->next = node;
}

ElemType Pop(LinkedStack S){
  if(!S) FatalError("Null Pointer");
  LinkedStack node = S->next;
  if(!node) FatalError("Underflow");
  val = node->data;
  S->next = node->next;
  return val;
}

1.2.4 应用与解题

【例】括号匹配

1.3 队列

1.3.1 特点

队列（queue）只允许在队尾（rear）进行插入，在对头（front）进行删除。

数组可以使用任意线性表实现。

1.3.2 链表实现

直接使用单链表实现，使用指针指示对头和队尾。头指针为队头 front，尾指针为队尾 rear 即可。

# Python 实现
class LinkedList:
	def __init__(self, val=0, next_node=None):
		self.data = val
		self.next = next_node
        
class Queue:
    def __init__(self):
        # 头指针和尾指针一开始均指向头结点
        self.rear = self.front = LinkedList()
                
    def push(self, key):
        self.rear = self.rear.next = LinkedList(key)
    
    def pop(self):
        node = self.front.next
        if not node:
            raise IndexError("[Underflow] Queue is empty")
        val = node.data
        self.front.next = node.next
        return val

// C 实现
typedef struct ListNode{
  ElemType data;
  struct ListNode *next;
} ListNode;

typedef struct Queue{
  ListNode *front;
  ListNode *rear;
} *Queue;

Queue NewQueue(){
  /* 新建一个有表头的链表 */
  ListNode *header = (ListNode *)malloc(sizeof(ListNode));
  if(!header) FatalError("Out of Space");
  header->next = NULL;
  Queue queue = (Queue)malloc(sizeof(struct Queue));
  if(!queue) FatalError("Out of Space");
  queue->front = queue->rear = header;
  return queue;
}

bool QueueEmpty(Queue Q){
  return Q->front->next;
}

void Push(Queue Q, ElemType x){
  if(!Q) FatalError("Null Pointer");
  ListNode *node = (ListNode *)malloc(sizeof(ListNode));
  if(!node) FatalError("Out of Space");
  node->data = x;
  node->next = NULL;
  Q->rear = Q->rear->next = node;
}

ElemType Pop(Queue Q){
  if(!Q) FatalError("Null Pointer");
  ListNode *node = Q->next;
  if(!node) FatalError("Underflow");
  val = node->data;
  Q->next = node->next;
  return val;
}

1.3.3 数组实现（循环数组）

数据存储在数组 queue[] 中，变量 front 为队头下标，变量 rear 为队尾下标，变量 size 为队列长度。而数组的长度，即为队列的最大长度。

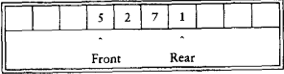
50CAD7BE-DB94-42B4-9BD5-227643800E90

出队时，返回 queue[front]，size 减一，front 后移。

入队时，size 加一，rear 后移，赋值给 queue[rear]。

当 front/rear 未到数组末端时，后移意为 front++/rear–；

当 front/rear 到达数组末端时，后移意为将其绕回数组开头，即使得front=0/rear=0。从而实现循环数组。

# Python 实现
class Queue:
    def __init__(self, maxsize):
        self.queue = [0] * maxsize
        self.maxsize = maxsize
        self.front = 0
        self.rear = -1
        self.size = 0
        
    def dequeue(self):
        if self.size==0:
            raise IndexError("[Underflow] Queue is empty")
        self.size -= 1
        val = self.queue[self.front]
        self.front += 1
        if self.front == self.maxsize:
            self.front = 0
        return val
    
    def enqueue(self,x):
        if self.size==self.maxsize:
            raise IndexError("[Overflow] Queue is full")
        self.size += 1
        self.rear += 1
        if self.rear == self.maxsize:
            self.rear = 0
        self.queue[self.rear] = x

// C 实现
typedef struct Queue{
  ElemType array[MAXSIZE];
  int front;
  int rear;
  int size;
} *Queue;

Queue NewQueue(){
  Queue queue = (Queue)malloc(sizeof(stuct Queue));
  queue->front = 0;
  queue->rear = -1;
  queue->size = 0;
  return queue;
}

void EnQueue(Queue Q, x){
  if(!Q) FatalError("Null Pointer");
  if(Q->size==MAXSIZE) FatalError("Overflow");
  Q->size++;
  Q->rear++;
  if(Q->rear==MAXSIZE) Q->rear = 0;
  Q->array[Q->rear] = x;
}

ElemType DeQueue(Queue Q){
  if(!Q) FatalError("Null Pointer");
  if(Q->size==0) FatalError("Underflow");
  Q->size--;
  val = Q->array[Q->front];
  Q->front++;
  if(Q->front==MAXSIZE) Q->front = 0;
  return val;
}

1.3.4 应用与解题

【例】两个栈模拟队列

略。

<推广> 本站使用 NameSilo 提供的域名服务。

泊书湾

写给自己看的算法书（一）

第1章线性表、栈、队列

1.1 线性表

1.1.1 顺序表

1.1.2 链表

1）头指针和头节点

2）单向链表

3）双向链表

4）循环链表

【例】约瑟夫环

【例】判断链表是否有环

5）静态链表

1.2 栈

1.2.1 特点

1.2.2 数组实现（通常使用该方式）

1.2.3 链表实现（链栈）

1.2.4 应用与解题

【例】括号匹配

1.3 队列

1.3.1 特点

1.3.2 链表实现

1.3.3 数组实现（循环数组）

1.3.4 应用与解题

【例】两个栈模拟队列

第1章 线性表、栈、队列

1.1 线性表

1.1.1 顺序表

1.1.2 链表

1）头指针和头节点

2）单向链表

3）双向链表

4）循环链表

【例】约瑟夫环

【例】判断链表是否有环

5）静态链表

1.2 栈

1.2.1 特点

1.2.2 数组实现（通常使用该方式）

1.2.3 链表实现（链栈）

1.2.4 应用与解题

【例】括号匹配

1.3 队列

1.3.1 特点

1.3.2 链表实现

1.3.3 数组实现（循环数组）

1.3.4 应用与解题

【例】两个栈模拟队列

第1章线性表、栈、队列